How to generate fibonacci sequence in parallel using spark
Fibonacci is basically this sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
The next number is found by adding the previous two numbers in sequence. The first two numbers are 0, 1.
Third number: 0 + 1 = 1
Forth number = 1 + 1 = 2
Fifth number = 1 + 2 = 3
Sixth number = 3 + 2 = 5
And so on…
Though it is obvious that you would not be able to parallelize this because the next number depends on previous.
There is an alternative formula of calculating the nth Fibonacci sequence:
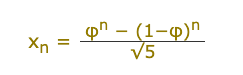
where " φ " is called the golden number which is approximately 1.618034…
Using this we can parallelize the calculation of first n fibobaci numbers.
Here is a code that you can run on pyspark console in CloudxLab:
import math
nums = sc.parallelize(range(1000))
golden_ratio = 1.618034
igolden_ratio = 1 - golden_ratio
sqrt5 = math.sqrt(5)
def fib(n):
fib_double = (golden_ratio**n - igolden_ratio**n)/sqrt5
return int(fib_double)
fibs = nums.map(fib)
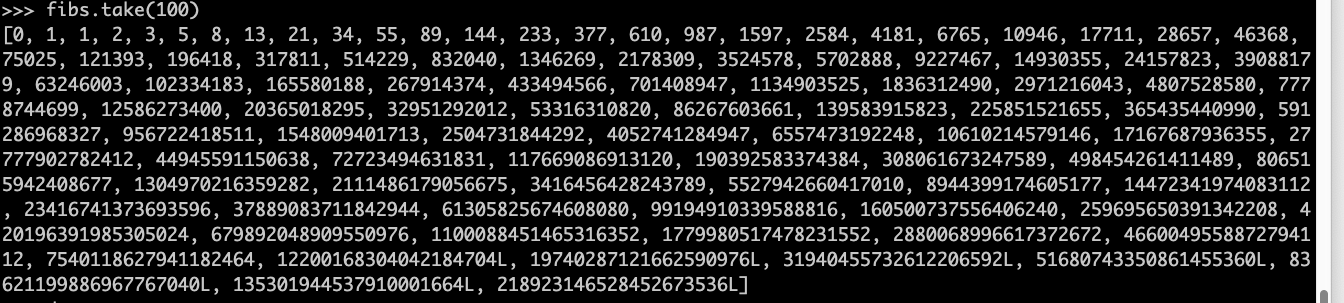
fibs.take(100)
You will get the following result.
Since calculation using golden number formula is costly, so a better idea will be to write a function which compute the fibonacci series using a list of indexes. For first two element of partition, we will compute the fibonicci sequence numbers using the golden number formula and for the rest we will generate the numbers sequentially. Since each partition is anyway processed sequentially, it would not make any difference. Here you go.
import math
golden_ratio = 1.618034
igolden_ratio = 1 - golden_ratio
sqrt5 = math.sqrt(5)
def fib(n):
print("GOLDEN Ration: ", n)
fib_double = (golden_ratio**n - igolden_ratio**n)/sqrt5
return int(fib_double)
# Test
# fib(0); fib(1); fib(2); fib(3)
def fib_seq(a):
print("----")
result = []
i = 0
for e in a:
if i <= 1:
result.append(fib(e))
else:
result.append(result[i-1] + result[i-2])
i += 1
return iter(result)
# Test
# list(fib_seq(range(5))) should print [0, 1, 1, 2, 3]
nums = sc.parallelize(range(1000))
fibs = nums.mapPartitions(fib_seq)
fibs.take(100)
fibs.getNumPartitions()
This is how it looks to me.