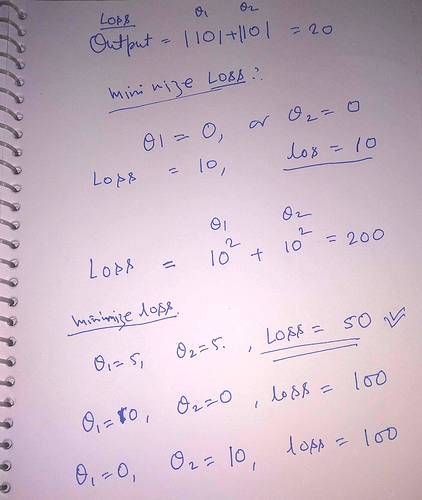Difference between L1 and L2 regularization in regression?

[sgiri]

In order to bring down the overfitting or variance, we use the regularization term in our cost function. There are three types of regularizations:

1. Ridge
2. Lasso
3. ElasticNet

The main objective here is to bring the freedom down by putting constraints on the weights. Basically, we force the model to keep the weights as small as possible. This is done by modifying the cost function such that the cost is higher when the weights are higher.

We understand that in the Ridge Regularization, we add summations of squares of all weights while in Lasso, we add the total of absolute values ( e.g. -3.5 => 3.5 and 4.1 => 4.1) of weights to the cost function. The Elastic Net is a combination of both Ridge and Lasso - it has the sum of squares as well as the absolute values of the weights in loss or cost function.

What exactly is the difference in the outcomes of Ridge and Lasso? And Why?

[sgiri]

The main difference in outcomes is that the models in Lasso regression are more sparse - meaning some of the weight could just become zero and hence the features to which these weights multiply to might disappear entirely. So, Lasso can act like a feature selector. On the other hand in the ridge regression, decreasing the various weights more uniformly is favored over making few weights disappear completely.

The question is Why?

This is how the cost/loss function in Ridge regression (or L2 regularization), Lasso (or L1 regularization) and Elastic Net looks like:

Now, let us look at loss due to regularization terms of both Ridge and Lasso. Say we have two weights theta1 and theta2 each with value 10 and we need to minimize the loss by reducing weights by 10.

In Lasso, The loss due to regularization term would be 20. If you reduce either theta1 or theta1 by 10, the overall loss will be the same i.e. 10.

But in Ridge, the loss due to regularization term would 200. And the loss will be minimum (= 50) when both theta1 and theta2 will be minimized equally instead of either one (= 100).

[satyajit_das]

Crisp and easy explanations. Sir. Mathematically gives more insights and make perfect sense!
Thanks for the article!