How to choose the dimensions of dense layer of cnn architectures??
Like in the above architecture for LeNet-5 dense layers are 120 and 84
and in AlexNet dense layers are 9216(multiplication of all dimensions of previous layer), 4096 and 4096.
So please tell me how to choose the dimensions of ending dense layers for cnn architecture??
1) The dimensional is calculated on the basics of inputs dimension and kernel/filter used..
a)
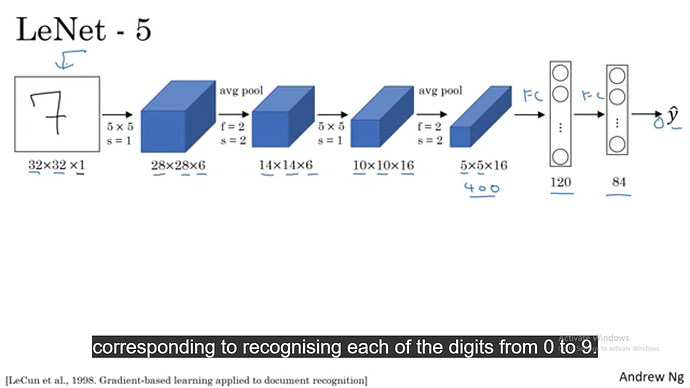
In LeNet-5 dense layers are 120 and 84 because.
The 3rd layer is a Conv layer of 10x10x16 --> average pooling layer --> Fully connected** layer, —> fully connected layer.**
Note :- The formula for the getting the next dimension when a pooling layer is
((input - filter size/stride) ) +1 = ((10 -2)/2)+1 = 5
and the pooling layer does not affect the depth, it only affects the length and breadth.
so the output architecture will be from 10x10x16 --> 5x5x16. flattened to 400x1
b) Later it has the fully connected layer.
The out dimension of the fully connected layer depends on the weights matrix that need to be multiplied with the inputs, so as per the matrix multiplication rule.
inputs = 400x1
weights matrix dimension = 120x400 as we want the output dimension of 120.
so, (120x400)x(400x1) = 120x1 dimension layer .
c) since we want the output layer dim as 84 so the weights matrix for the fully connected layer will be 84x120
(84x120)x(120x1) = 84x1 dimension output.
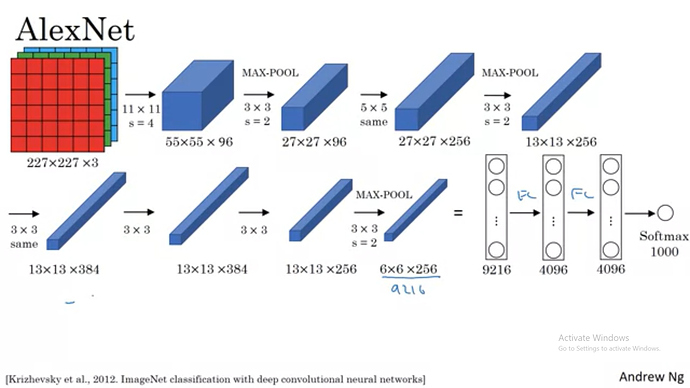
2) Similarly in the ALEXNET also.
a) The 13x13x256 -> with a max- pooling layer of 3x3 and stride of 2 will give the output as ((13-3)/2 )+1 = 6
so output dimension will be 6x6x256 = 9216 ( as pooling layer don’t affect the depth).
b) This 6x6x256 will be then flattened into 9216 neurons. Then a fully connected layer
so the weight matrix will be (4096x9216) this you have to decide.
(4096x9216)x(9216x1) = (4096x1).
c) (1000x4096)x(4096x1) = 1000 neurons at the output.
So, therefore ALEXNET has 1000 classes at the output.
All the best!
